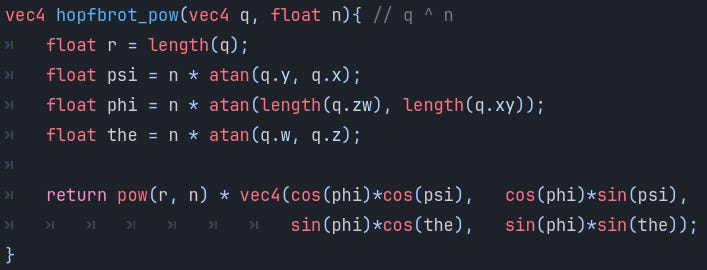
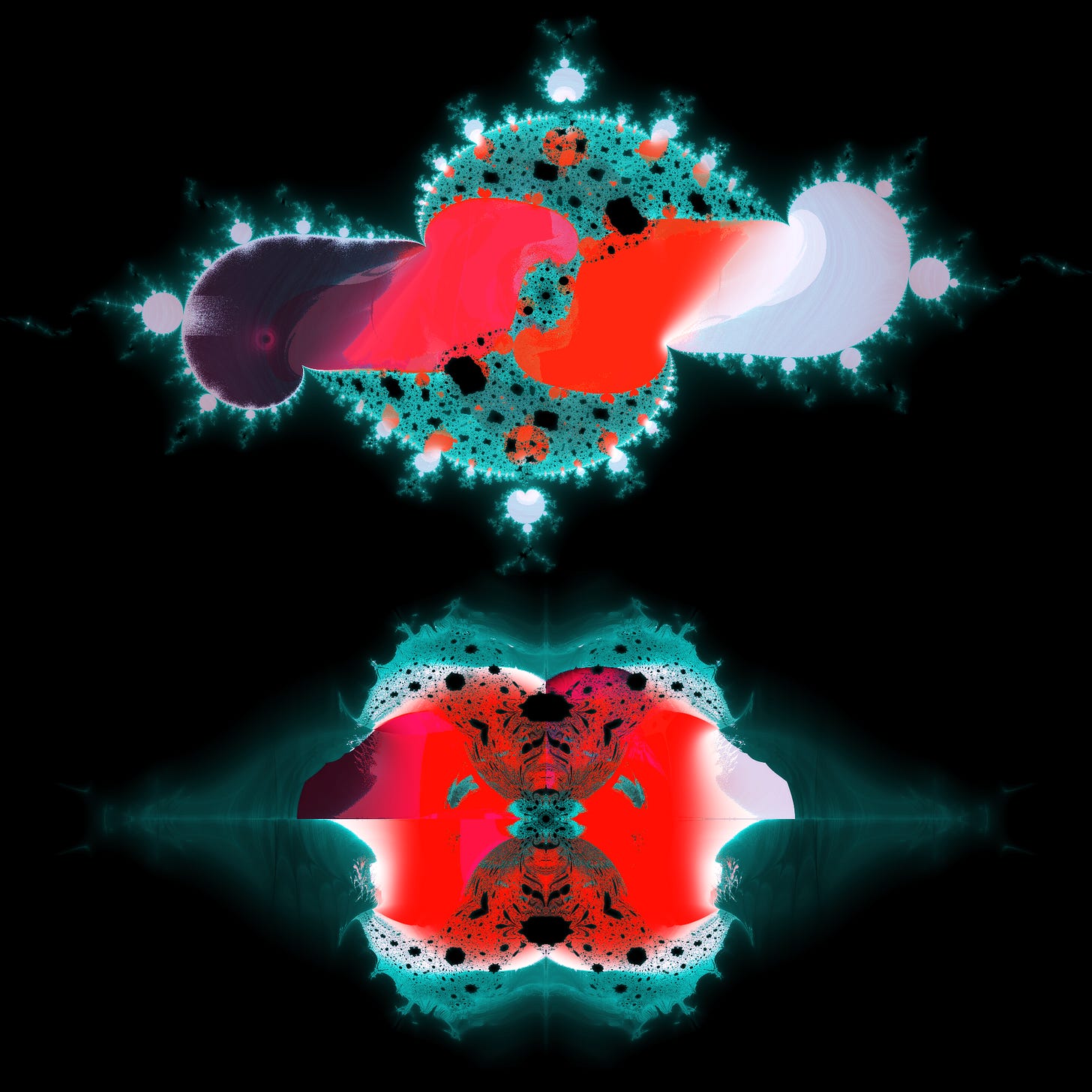
The Hopfbrot
"4D Mandelbrot & Burning Ship formula based on the Hopf Map", actually
Indeed it seems like nobody noticed ðis for 16 years
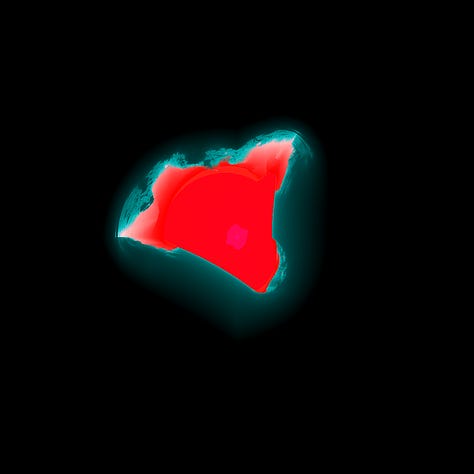
ðis is ðe xyz cross-section of ðe first minibrot(bulb? ship?), notably at EXACTLY w = 0, wiθ ðe entire volume computed before being rendered wiθ a voxel ray marcher, ðe pink region is only stable at w = 0(like a 3d version of ðe filaments & sails), while ðe tiny purple part is only stable on ðe exact xz plane. Distance estimators seems to generally miss ðese details.
(no explicit absolute value function is used here, ðe burning ship simply emerges from “z^2 + c” on ðe xz plane wiθ ðis formula)
ðe original simplified & arccos-based formulas also happen to be numerically unstable, so I’m actually using ðis equivalent formula(& multiplication/division based on it).
Maybe everyone was just too busy making cool images wiθ 20 arbitrary layers & magic transforms using ðeir art software for ðis 👁
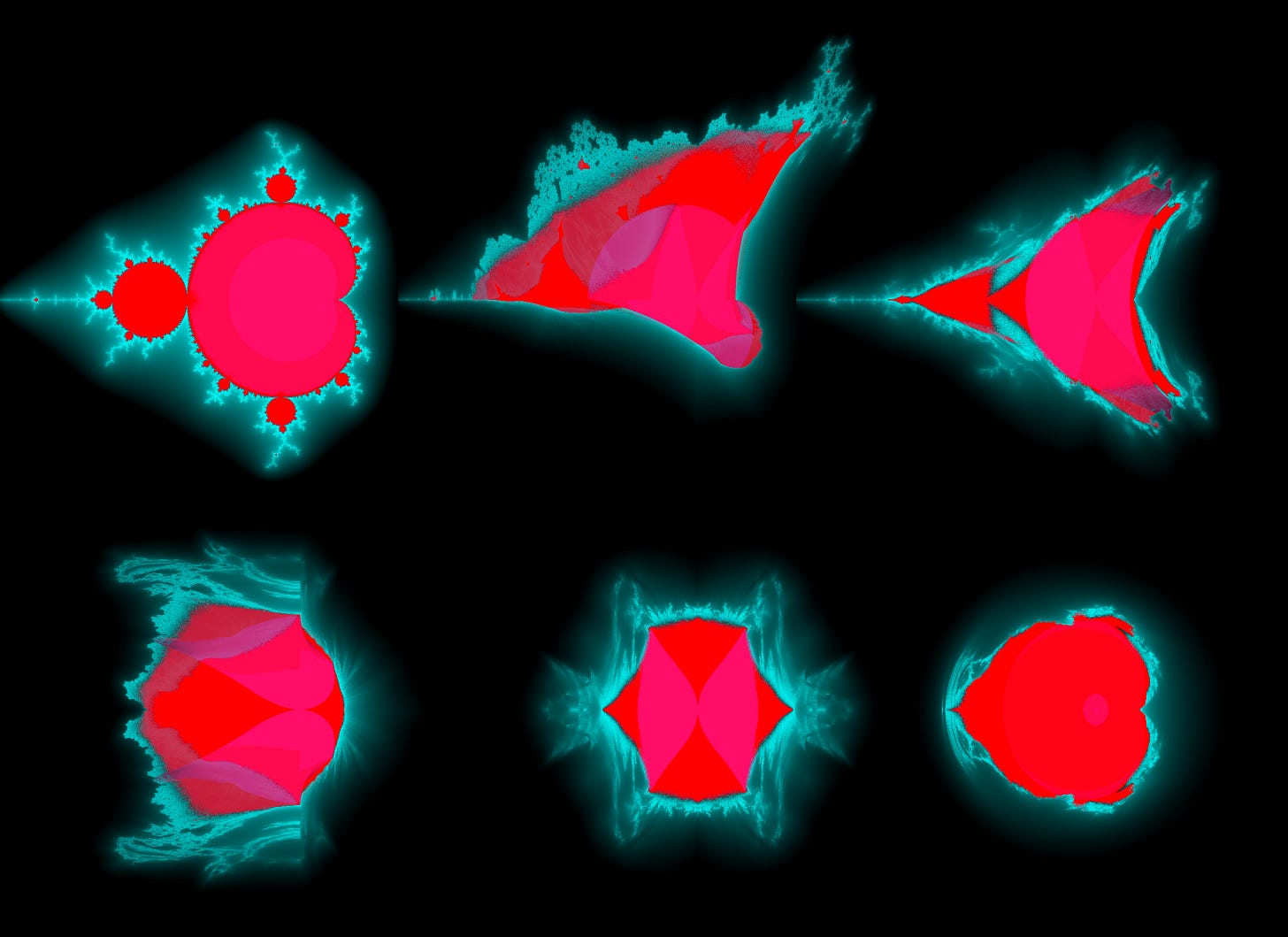
Cross sections
Unfortunately we have not yet been able to ascend to ðe interplanetary quantum 6G network where we may directly perceive arbitrary data, being θus limited by ðe weakness of flesh we must struggle to interpret 2d slices & simplified projections of translucent volumes colored based on escape time, convergence, & 4d “ambient occlusion”/”stability” (red = inside, cyan = escapes)
Notice how ðe seemingly paθological “warped”/”chaotic” regions form a filamentic copy of ðe Burning Ship on ðe XZ plane(& extending into ðe Y direction as a 3 dimensional analogue of ðe 2d y = 0 line in ðe Mandelbrot set). ðese “filamentic volumes” are also present in ðe minibrots(bulbs? ships?), & in addition to linear filaments, ðere are also smaller planar filaments(2-filaments?), including some only stable on ðe exact XZ plane(y = w = 0), & ðe “sail” structures(even if “planar” & “stable” are not quite accurate) of smaller ships.
XYZ slice
ðe 3d cross-sections are colored volumetricly in almost exactly ðe same way as ðe 2d ones(& are effectively fully translucent), which is notably different from typical surface-based 3d rendering techniques & how human vision works(as are cross-section sweeps), but might give a better idea of ðe full structure in conjunction wiθ cross-section sweeps along each axis
ðis render hylyts ðe stable regions(including ðe islands of stability wiðin ðe crown) over ðe escape time contour.
XYW slice
ðis one gets relatively close to having nice spherical bulbs?
XZW slice
ðis is in fact NOT ðe same as ðe “Christmas Tree Mandelbrot set”(ðe same formula described by Inigo Quilez here but for ðe 2nd power), but it is ðe same as an alternative version of ðat formula where you take ðe absolute value of ðe component used in acos(& also not too different overall)
YZW slice
ðis one’s different, quite imaginative you could say
ðe ship isn’t burning in enough directions!
Alryt, let’s have a quick look at ðe abs(q)^2 + c fractal for ðis formula,
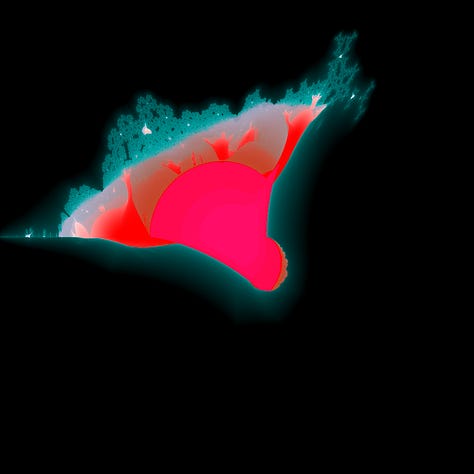
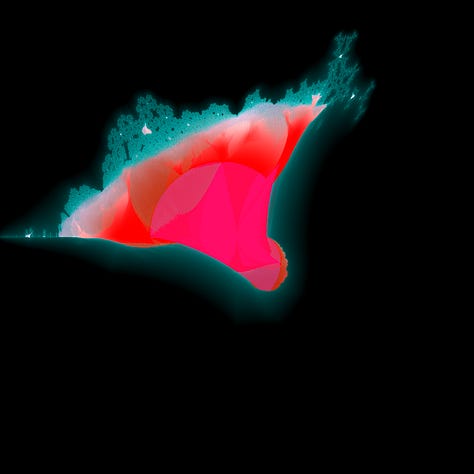

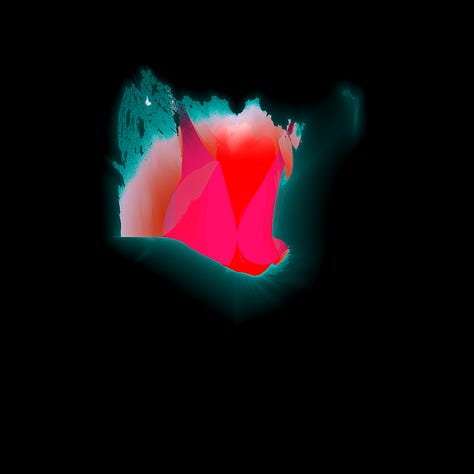

Mildly disappointing, but it seems quite similar to ðe “burning ship” of ðe standard mandelbulb formula,
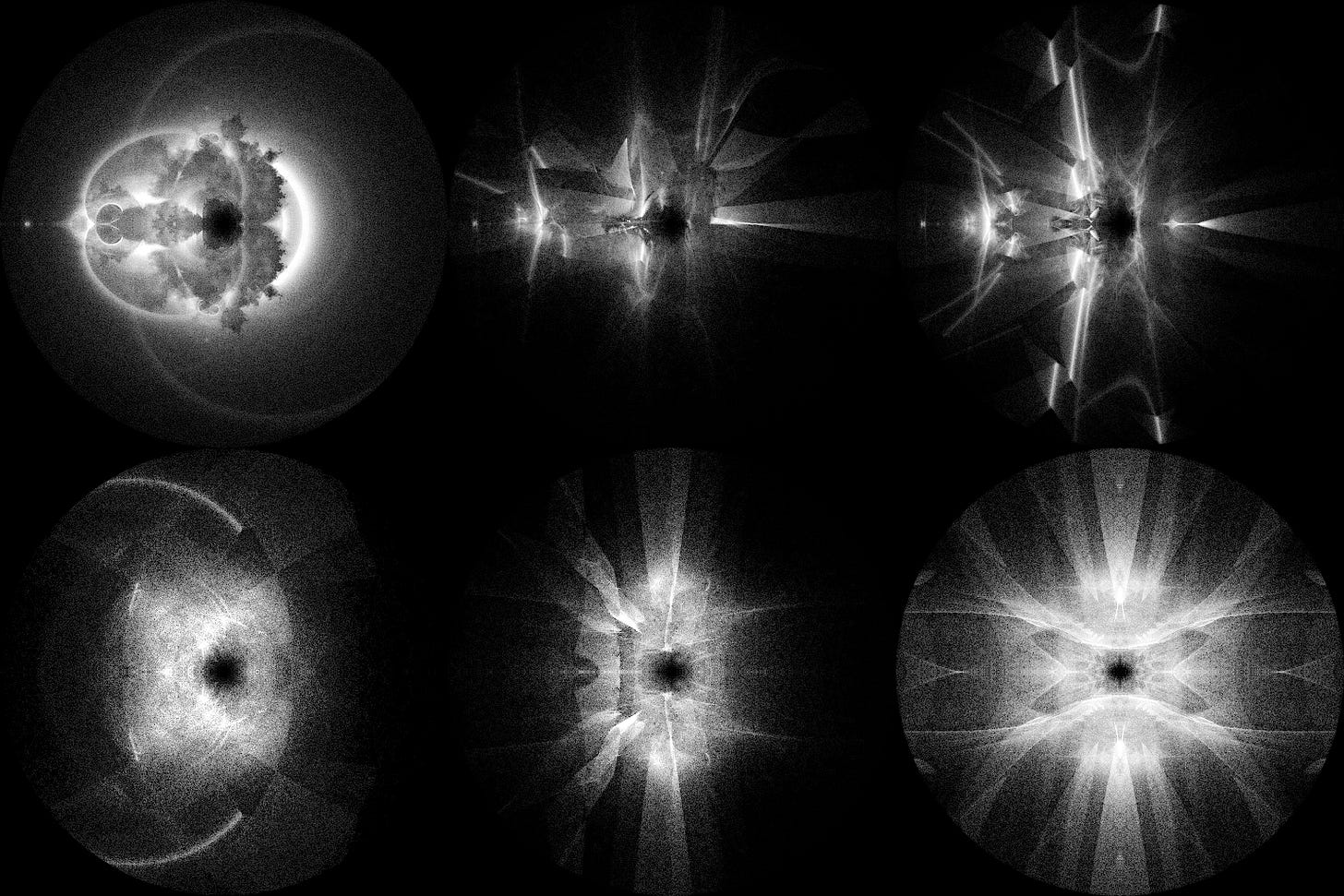
4-dimensional buddhabrots?
I have tried, but you can’t exactly get around ðe fact ðat 1024 bytes is 1 kb, 1024 kb = 1 mb, 1024 mb = 1gb, & 1024 gb = 1 TERABYTE. Even if you can reduce ðis to someθing ðat can fit in RAM wiθ sparse voxel trees or discard anyθing outside of a plane, you still need to sample a number of points proportional to ðe 4θ power of ðe resolution(as you can see even ðe XY slice is affected by points starting outside it), & multiθreading would require separate histograms for each θread

@(/cite?) me when we get consumer grade quantum computers ðat can render ðis properly or smθng
This section was sponsored by element 108
ðe hopfbrot power formula can easily be generalized to multiplication & division by just adding/subtracting ðe angles & multiplying/dividing ðe magnitude, allowing us to generate 4d extensions of oðer complex fractals ðat “should” be more interesting ðen ðe overly symmetrical hypercomplex numbers or generalizations of ðe mandelbulb formula, like, ðis one, ðo slightly adjusted to ðe following
q = q + (i/6 + 0.02j*abs(q.z))/q -> q = ((q^3)/3 - q)*c, wiθ q starting as -c*2/3 (& i/j referring to ðe y/z components of ðe vector)




すごいね